I now use q emulator, which is a free program that allows you to run windows applications within osx, however, this can be slow, and is defeating the point of having a mac in the first place.
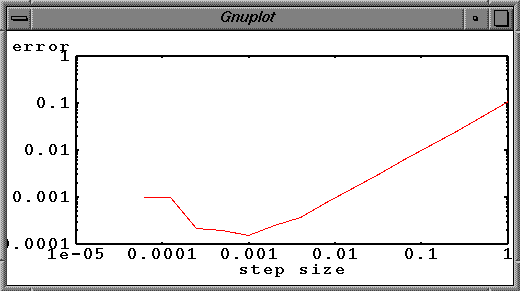
Program test implicit none real(8)::a,b,h,y_0,t write(*,*)'Enter the interval a,b, the value of the step-size h and the value of y_0' read(*,*)a,b,h,y_0 open(unit=1, file='resultadoEuler.dat',status='old') call euler(y_0,a,b,h) close(1) contains subroutine euler(y_0,a,b,h) implicit none real(8), intent(inout)::a,h,b, y_0 real(8):: y,t t=a y=y_0 do while(t. Program solvingwithRungeKutta implicit none real(8)::a,b,h,y_0,t write(*,*)'Enter the interval a,b, the value of the step-size h and the value of y_0' read(*,*)a,b,h,y_0 open(unit=1, file='resultadoRungeKutta.dat',status='old') call RungeKutta(y_0,a,b,h) close(1) contains subroutine RungeKutta(y_0,a,b,h) implicit none real(8), intent(inout)::a,h,b, y_0 real(8):: y,t, F_1, F_2, F_3, F_4 t=a y=y_0 do while(t. Program test2 implicit none real(8)::a,b,h,y_0,t,y, pi write(*,*)'Enter the interval a,b, the value of the step-size h and the value of y_0' read(*,*)a,b,h,y_0 open(unit=32, file='valores_exactos.dat') pi=acos(-1d0) t=a do while (t. What does the graph of the non-combined routines look like?I don't have the errors in my first codes.
The Runge-Kutta method is the most widely used method of solving. A fortran 90 program to solve ordinary differential equation by runge-kutta method.
However I do have the exact values versus the calculated value for each methods. I send 2 pictures. One more or less general and the other around where I should have noticed the biggest value of error for Runge-Kutta's method. This is actually convincing myself that Euler's method doesn't seem that bad at all, even with a small h. I'll try right now with a small h (around 4 or 5 divisions) and post some pics. I'm not sure what the issue with the combined programs is, but if you want to try another method, the link below is to a description of an iterative (predictor + corrector) method. You could try doing 4 iterations (the initial Euler + 3 trapezoidals, (y [3])) to compare with Runge-Kutta with about the same overhead.
With more iterations, this method will converge to specific values for each step, but since it's a linear approximation for each step (trapezoidal), you still need to keep h relatively small. I'm not sure what the issue with the combined programs is, but if you want to try another method, the link below is to a description of an iterative (predictor + corrector) method. You could try doing 4 iterations (the initial Euler + 3 trapezoidals, (y [3])) to compare with Runge-Kutta with about the same overhead.
With more iterations, this method will converge to specific values for each step, but since it's a linear approximation for each step (trapezoidal), you still need to keep h relatively small. Thank you for your help. I'm going to check this out tomorrow, I'm off to bed now (over 2 am). My last thoughts for today is that not only the program that merges both codes is wrong for Runge Kutta but even my Runge Kutta (2nd code of 1st post) MUST be wrong. I hate it when I have an error that is so small that I discover it only after looking for hours on what's wrong:/. Some news: I've written a few other codes (also with another methods to solve ODE).
I plotted the error for Euler, Heun and Runge-Kutta's methods. One thing I know for sure now is that there's something wrong in all my codes when it comes to Runge Kutta. For another ODE than the one here, I've tested Runge-Kutta's method along with Heun and Euler. The interval was [0,10] and the step size was 0.1. Euler was more efficient than Heun by a few. Runge-Kutta's error was almost exactly the same as Heun for all points. It means my Euler's method is more efficient than my Runge-Kutta's one.
0 kommentar(er)
